DİRENÇ DEVRELERİ
SERİ DİRENÇLER - ÇÖZÜMLÜ ÖRNEK - 3
ÖRNEK-3
Aşağıdaki bağlantılarda tüm dirençlerin
- üzerlerindeki voltajları ve
- üzerlerinden geçen akımları
bulalım.
a)

b)

c)

ÇÖZÜM
a)
Seri bağlı dirençler üzerinden aynı miktarda ve aynı yönde akım geçer. Ayrıca, bu akım, seri bağlı dirençlerin yerine koyduğumuz eşdeğer direnç üzerinden geçen akımla da aynıdır.
Eşdeğer direnç Reş = 1 kΩ + 1 kΩ + 1 kΩ = 3 kΩ'dur.

Ohm Kanunu'nu kullanarak eşdeğer direnç üzerinden geçen akımın 3 mA olduğunu görebiliriz.
......
Eşdeğer direnç üzerinden geçen akım, seri bağlı her bir direnç üzerinden geçen akıma eşittir.

Direnç değerlerini ve üzerlerinden geçen akımları bildiğimize göre, Ohm Kanunu'nu kullanarak üzerlerindeki voltajları da bulabiliriz.
V1 = 3 mA × 1 kΩ = 3 V
V2 = 3 mA × 1 kΩ = 3 V
V3 = 3 mA × 1 kΩ = 3 V

b)
Bu soruyu çözerken de bir önceki devre için uyguladığımız yöntemi kullanıyoruz.
- Önce eşdeğer direnci bulup devredeki seri dirençlerin yerine bu direnci koyuyoruz.
- Daha sonra Ohm Kanunu'nu kullanarak, eşdeğer direnç üzerinden geçen akımı buluyoruz.
- Eşdeğer direnç üzerindeki akım, seri dirençlerdeki akıma eşit olduğu için bu akımı ve direnç değerlerini kullanarak her bir direnç üzerindeki voltajı buluyoruz.
Devredeki tüm dirençler seri bağlı olduğu için eşdeğer direnci bulabilmek için direnç değerlerini toplarız.
Reş = 1 kΩ + 2 kΩ + 3 kΩ = 6 kΩ

Eşdeğer direncin üzerindeki akımı Ohm Kanunu'nu kullanarak bulabiliriz.
......
Buna göre, devredeki tüm dirençlerin üzerinden 1 mA akım geçtiği sonucunu çıkarabiliriz. Ohm Kanunu'nu bir defa daha kullanarak dirençlerin üzerindeki voltajları bulabiliriz..
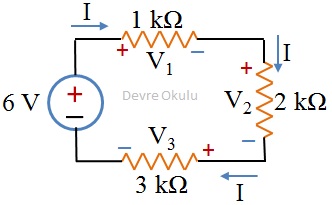
V1 = 1 mA × 1 kΩ = 1 V
V2 = 1 mA × 2 kΩ = 2 V
V3 = 1 mA × 3 kΩ = 3 V
c)
Bu bağlantıdaki tüm dirençler de seri bağlıdır ve üzerlerindeki akımlar eşittir. Daha önce olduğu gibi bu devrede de eşdeğer direnci bularak çözüme başlayabiliriz.
Reş = 5 kΩ + 10 kΩ = 15 kΩ
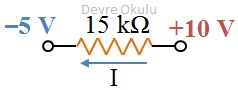
Eşdeğer direnç üzerindeki akımı bulabilmek için, öncelikle üzerindeki potansiyel farkını hesaplamamız gerekiyor. Sol terminalin potansiyeli –5 V ve sağ terminalin potansiyeli +10 V olduğu için eşdeğer direnç üzerindeki toplam potansiyel farkı 10 – (–5) = 15 V'tur.
......
Buna göre 5 kΩ ve 10 kΩ'luk dirençler üzerinden de 1 mA akım geçer. V = IR formülünden üzerlerindeki voltajları da bulabiliriz.

V1 = 1 mA × 5 kΩ = 5 V
V2 = 1 mA × 10 kΩ = 10 V