KONU 4-SERİ DİRENÇLER
BÖLÜM 3-SERİ BAĞLANTIDA POTANSİYEL DAĞILIMI
Seri bağlı dirençler, toplam potansiyel farkını direnç değerleriyle doğru orantılı olarak paylaşırlar.
SERİ BAĞLANTIDA VOLTAJ FORMÜLÜ
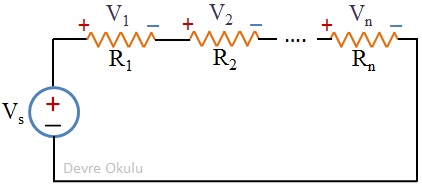
Seri bağlı R1, R2, ..., Rn dirençlerinin toplam voltajı Vs ise, Ri direncinin üzerindeki voltaj aşağıdaki formülle bulunabilir.
... ...
Yukarıdaki denkleme göre bir direncin değeri, seri bağlı olduğu dirençlere oranla ne kadar yüksekse üzerindeki voltaj da o kadar yüksek olur.
ÖRNEK:
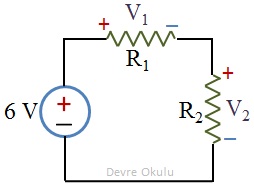
a) R1 = R2 = 1 kΩ
b) R1 = 2 kΩ, R2 = 1 kΩ
c) R1 = 4 kΩ, R2 = 2 kΩ
Yukarıdaki üç farklı durum için R1 ve R2 dirençleri üzerindeki voltajları bulalım.
Voltaj kaynağı tüm durumlarda sabit 6 V voltaj sağladığı için dirençler üzerindeki toplam potansiyel farkı bu durumların tümünde 6 V'tur.
Ayrıca, verilen devrede seri bağlı 2 direnç olduğu için formülün paydasına R1 + R2 yazmamız gerekir. Buna göre, R1 ve R2 üzerindeki voltaj değerleri
... ve ...
formülleriyle bulunabilir.
a) İlk durumda dirençlerin değerleri eşit olduğundan 6 V'u eşit şekilde paylaşırlar. Formül kullanmadan da her bir direnç üzerindeki voltajın 3 V'a eşit olduğunu söyleyebiliriz.
V1 = 3 V ve V2 = 3 V
Değerleri formülde yerlerine koyarak sonuca ulaşmak istiyorsak, Vs yerine 6 V, R1 ve R2 yerine 1 kΩ yazmamız gerekir.
... ...
... ...
b) İkinci durumda, R1 direnci R2'nin 2 katıdır. Buna göre, 6 V'u paylaşırken R1'in üzerinde R2'nin 2 katı kadar voltaj olması gerekir. Toplam voltajın 6 V olması gerektiği için bu şarta uyan değerler V1 = 4 V ve V2 = 2 V'tur.
Vs = 6 V, R1 = 2 kΩ ve R2 = 1 kΩ değerlerini formülde yerlerine yazarak da aynı sonucu elde edebiliriz.
... ...
... ...
c) Son durumda, R1 direncinin yine R2'nin 2 katı olduğunu görüyoruz. Buna göre, bir önceki durumda olduğu gibi V1 = 4 V ve V2 = 2 V olması gerekir. Formül de bizr aynı sonucu verecektir.
... ...
... ...
b ve c durumlarında dirençler farklı olduğu halde aynı sonuçlarla karşılaşıyoruz. Seri dirençlerde voltaj paylaşımı yaparken önemli olan şey, dirençleri değeri değil, oranıdır. Bu oranlar b ve c durumlarında aynı olduğu için voltajlar aynı çıkıyor. Bu iki devrede farklı olan şey dirençler üzerinden geçen akımdır.
TÜM DİRENÇLER EŞİTSE
Seri bağlı eşit dirençler, toplam voltajı eşit paylaşırlar. Bir direncin üzerindeki voltajı bulabilmek için toplam voltajı direnç sayısına bölebiliriz. Örneğin, 20 V kaynağa bağlı olan 10 eşit direncin her birinin üzerindeki potansiyel farkı, ... = 2 V'tur.
DİRENÇLERDEN BİRİ ÇOK BÜYÜKSE
Seri bağlı dirençlerden biri diğerlerine göre çok büyükse, bu direncin yaklaşık olarak tüm voltajı üzerine aldığını varsayabiliriz. Örneğin, 9 V kaynağına 5 Ω ve 5 MΩ'luk dirençlerin seri bağlandığını düşünelim. Hesap yapmadan, 5 MΩ'luk direncin üzerindeki voltajın yaklaşık olarak 9 V olduğunu söyleyebiliriz. Değerleri formülde yerine koyduğumuzda da sonucun 9 V'a çok yakın olduğunu görebiliriz.
... ...
SERİ DİRENÇLERİN VOLTAJ FORMÜLÜ NEREDEN GELİYOR?
Seri dirençlerin voltaj formülünü Kirchhoff Voltaj Kanunu ve Ohm Kanunu'nu kullanarak elde edebiliriz.
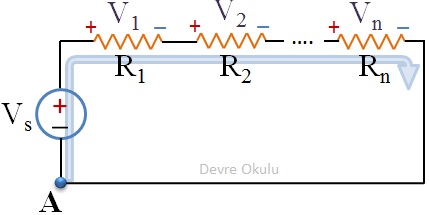
Seri bağlı n tane direncin Vs potansiyel farkı oluşturan bir voltaj kaynağına bağlandığını düşünelim. A noktasından başlayarak, saat yönünde, tekrar aynı noktaya ulaşıncaya kadar karşılaştığımız devre elemanlarının voltajlarını toplayıp, 0'a eşitleyelim.
Bu voltajları yazarken, önüne ilk karşılaştığımız işareti (+ veya –) koymayı unutmayalım.
–Vs + V1 + V2 + ... + Vn = 0
–Vs'yi karşı tarafa +Vs olarak atalım.
V1 + V2 + ... + Vn = Vs
Seri bağlı dirençlerin üzerinden akan ortak akıma I dersek, Ohm Kanunu'nu kullanarak, her bir direnç üzerindeki akım ve direnç cinsinden aşağıdaki gibi yazabiliriz.
IR1 + IR2 + ... + IRn = Vs
Eşitliğin solundaki terimleri I parantezine alalım.
I(R1 + R2 + ... + Rn) = Vs
İki tarafı toplam dirence bölersek, seri dirençler üzerinden geçen akımı
...
olarak buluruz.
Seri bağlantıdaki herhangi bir Ri direncinin üzerindeki voltajı bulabilmek için direnç değeri ile bulduğumuz akımı çarparız.
... ... ...
Bölüm 1 - Bölüm 2 - Bölüm 3 - Bölüm 4