OPAMP DEVRELERİ

EVİREN YÜKSELTEÇ (INVERTING AMPLIFIER)

---

Bu yazıda, OPAMP ile yapılmış eviren yükselteç devresinin çıkış voltajını ve voltaj kazancını bulacağız. Eviren yükselteç ile ilgili çözümlü örnekleri Eviren Yükselteç-Çözümlü Örnekler sayfasında bulabilirsiniz.

Yukarıda, OPAMP kullanılarak yapılmış bir eviren yükselteç devresi görüyoruz. OPAMP’ın pozitif girişi toprağa, negatif girişi ise $\mathbf{R_{IN}}$ direnci üzerinden bir giriş voltajına bağlı. Çıkış ile negatif giriş arasında bir geribesleme direnci ( $\mathbf{R_{F}}$) bulunmakta. Yükseltecin kazancını, $\mathbf{R_{IN}}$ ve $\mathbf{R_{F}}$ dirençleriyle belirliyoruz. Bazı OPAMP'ların çalışabilmesi için biri pozitif bir negatif olmak üzere iki farklı besleme voltajı kullandığımız halde, bazı OPAMP'lar için pozitif bir besleme voltajı yeterli olacaktır.

Çıkış Voltajı:

---

OPAMP ile analiz yaparken karşımıza iki farklı model çıkıyor: ideal ve detaylı model. Bu yazıda ideal modeli temel alıyoruz.

Pozitif Giriş Voltajı, V_p

Bu devrede OPAMP'ın pozitif girişi, direk olarak toprağa bağlanmıştır. Bu nedenle, pozitif girişteki voltaj sıfırdır.

Negatif Giriş Voltajı, V_n

İdeal OPAMP'ın birinci varsayımına göre, pozitif ve negatif girişlerdeki voltajlar birbirine eşit olmalıdır. Buna göre,

V_n = 0

olur. Negatif giriş toprağa bağlı olmadığı halde, voltajı sıfır olduğundan toprak gibi davranır. Böyle noktalara sanal toprak (virtual ground) denir.

Giriş Akımı, I_IN

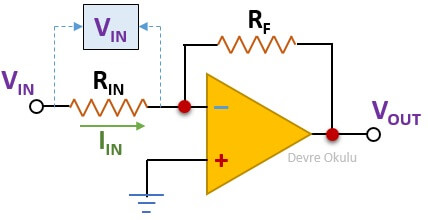
R_IN direncinin sol terminalindeki voltaj V_IN'e ve sağ terminalindeki voltaj 0 V'a eşittir. Buna göre, R_IN üzerindeki gerilim V_IN olur. Ohm Kanunu’nu kullanarak, I_IN akımının

olduğunu görebiliriz.

Geribesleme Akımı, I_F

Kirchhoff Akım Kuralı’na göre, bir noktaya giren akımlar toplamı, çıkan akımlar toplamına eşit olmalıdır. Sanal toprak olan noktaya giren tek akım I_IN , çıkan akımlar ise I_n ve I_F'dir. Kirchhoff Akım Kuralı'nı uygulayarak aşağıdaki eşitliği elde edebiliriz.

I_IN = I_F + I_n

İdeal OPAMP’ın ikinci varsayımına göre I_n sıfıra eşittir. Bu nedenle, I_F akımı I_IN'e eşit olmalıdır.

Çıkış Voltajı, V_OUT

Çıkış voltajı olan V_OUT'u bulabilmek için, şimdi R_F direncine konsantre olmamız gerekiyor. R_F üzerinden $\mathbf{\color{olive}I_{F}\color{black}=\dfrac{\color{purple}V_{IN}}{R_{IN}}}$ kadarlık bir akım geçiyor. Bu nedenle, R_F üzerindeki voltaj düşümü

$\mathbf{R_{F}I_{F}=R_{F}\dfrac{\color{purple}V_{IN}}{R_{IN}}}$

kadar olur. Pozitif akım her zaman yüksek voltajdan düşük voltaja doğru akar. I_F akımının yönüne dikkat edersek, direncin sol ucunun voltajı, sağ ucundan $\mathbf{R_{F}\dfrac{\color{purple}V_{IN}}{R_{IN}}}$ kadar fazla olmalıdır. Başka bir değişle, direncin sağ tarafındaki voltajı bulabilmek için sol taraftaki voltajdan $\mathbf{R_{F}\dfrac{\color{purple}V_{IN}}{R_{IN}}}$ çıkarmalıyız. Fakat, direncin soldaki ucu sanal toprağa bağlı olduğundan voltajı sıfırdır. Bu nedenle, direncinin sağ terminalinin voltajı

$\mathbf{0-R_{F}\dfrac{\color{purple}V_{IN}}{R_{IN}}}$ $\mathbf{=-R_{F}\dfrac{\color{purple}V_{IN}}{R_{IN}}}$

olur. Direncin sağ tarafı V_OUT'a bağlı olduğu için aşağıdaki eşitliği yazabiliriz.

Voltaj Kazancı

---

Bir devrede, çıkış voltajının giriş voltajına bölümüne Voltaj Kazancı (Voltage Gain) denir. Bu devrenin Voltaj Kazancı,

Doyum

---

Çıkış voltajı için bulduğumuz sonuç, yalnızca maksimum ve minimum çıkış voltajları arasında olduğunda geçerlidir.

İdeal bir OPAMP'ın maksimum çıkış voltajının pozitif besleme voltajına eşit olduğu düşünülebilir. Eğer, yukarıdaki formül bize maksimum voltajdan daha yüksek bir sonuç çıkarıyorsa, OPAMP pozitif doyuma ulaşmış demektir. Bu durumda, maksimum çıkış voltajına eşit olur.

Benzer şekilde, formül miminum çıkış voltajından daha düşük bir sonuç veriyorsa, çıkış voltajı, minimum çıkış voltajına eşit olur ve OPAMP negatif doyuma ulaşır.

İdeal koşullarda maksimum çıkış voltajı pozitif besleme voltajına eşit varsayılabilse de, gerçekte bu voltaja ulaşmamız pek mümkün değildir. Ayrıca, çıkış voltajının maksimum değeri, OPAMP'a bağlanan yüke bağlı olarak değişir.

İlgili Bağlantılar

---

EVİREN YÜKSELTEÇ EVİREN YÜKSELTEÇ-ÇÖZÜMLÜ ÖRNEKLER EVİRMEYEN YÜKSELTEÇ EVİRMEYEN YÜKSELTEÇ-ÇÖZÜMLÜ ÖRNEKLER

İlginizi Çekebilir

---