OPAMP DEVRELERİ
EVİRMEYEN YÜKSELTEÇ (NON-INVERTING AMPLIFIER)
Evirmeyen yükselteç ile ilgili çözümlü örnekleri Evirmeyen Yükselteç-Çözümlü Örnekler sayfasında bulabilirsiniz.
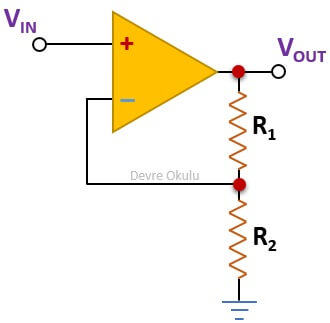
Yukarıda, OPAMP ile yapılmış bir evirmeyen yükselteç devresi görüyoruz. Bu devrede, giriş sinyali olan VIN'i OPAMP'ın pozitif girişine bağlıyoruz. Çıkış ile negatif giriş arasına R1 ve negatif giriş ile toprak arasına R2 direncini bağlıyoruz. Yükseltecin kazancını R1 ve R2 dirençleri ile belirliyoruz. Bazı OPAMP'ların çalışabilmesi için biri pozitif biri negatif olmak üzere, iki besleme voltajı vermemiz gerekirken; bazıları için tek bir pozitif besleme voltajı yeterli olacaktır.
Bu devrenin çıkış voltajını ve voltaj kazancını buluyoruz.
Çıkış Voltajı:
OPAMP devrelerinin analizini yaparken farklı matematiksel modeller kullanabiliriz. Bu sayfada en basit matematiksel model olan ideal modeli kullanıyoruz.

Ideal bir OPAMP için aşağıdaki varsayımları kullanıyoruz.
- Pozitif(+) ve Negatif(–) girişlerin voltajları eşittir.
- Pozitif ve negatif girişlerden OPAMP'a giren akımlar sıfırdır.
Vp = Vn
Ip = In = 0
Pozitif Giriş Voltajı, Vp

OPAMP'ın pozitif girişi, direk olarak giriş sinyali olan VIN'e bağlanmıştır. Bu nedenle, pozitif girişteki voltaj VIN'e eşittir.
Vp = VIN
Negatif Giriş Voltajı, Vn

İdeal OPAMP'ın ilk varsayımına göre, pozitif ve negatif girişlerdeki voltajlar eşit olmalıdır. Bu nedenle, Vn = VIN olur.
Vn = VIN
I2 Akımı

R2 direncinin üst terminalindeki voltaj VIN ve alt terminalindeki voltaj 0 V olduğu için, üzerindeki voltaj farkı VIN'e eşittir. Ohm Kanunu’nu kullanarak R2 üzerinden akımın
...
olduğunu görebiliriz.
...
I1 Akımı
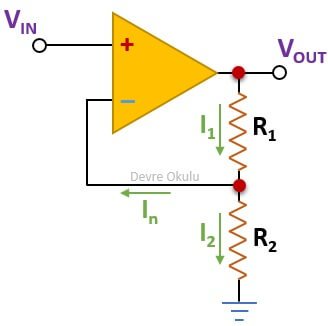
Kirchhoff Akım Kuralı’na göre, bir noktaya giren akımlar toplamı, çıkan akımların toplamına eşit olmalıdır. R1 ile R2 arasındaki düğümden çıkan akımlar I2 ve In; bu düğüme giren tek akım I1'dir. Bu nedenle,
I1 = I2 + In
olur. In = 0 varsayımından yola çıkarak aşağıdaki eşitliği yazabiliriz.
...
...
Çıkış Voltajı, VOUT

Evirmeyen yükseltecin çıkış voltajı, R1 ve R2 üzerindeki voltajların toplamına eşittir. R2 üzerindeki voltaj VIN'e ve R1 üzerindeki voltaj I1 . R1'e eşittir.
VOUT = VIN + I1 . R1
I1 yerine, yukarıdaki bulduğumuz formülü yazarsak
... ... ...
sonucunu elde ederiz.
Voltaj Kazancı
Çıkış voltajının giriş voltajına bölümüne Voltaj Kazancı (Voltage Gain) denir. Bu devre için voltaj kazancı aşağıda verilmiştir.
... ...
Evirmeyen yükseltecin voltaj kazancı, evirenin aksine pozitiftir. Ayrıca ... pozitif bir değer olduğundan, kazanç her zaman 1'den büyük çıkar.
Doyum
... ...
Yukarıda bulduğumuz sonuç, yalnızca VOUT'un maksimum ve minimum çıkış voltajları arasında olduğunda geçerlidir. Maksimum çıkış voltajından daha yüksek bulduğumuz değerler, OPAMP'ın pozitif doyuma ulaştığını ve çıkıştan maksimum voltajına eşit bir değer alınacağını gösterir. Benzer şekilde minimum çıkış voltajından daha düşük değerler almamız da mümkün değildir. Her ne kadar gerçekte bu değerler farklılık gösterse de, ideal modelde maksimum çıkış voltajının kabaca pozitif besleme voltajına eşit olduğunu kabul edebiliriz.