OPAMP DEVRELERİ
EVİRMEYEN YÜKSELTEÇ - ÇÖZÜMLÜ ÖRNEK - 1
Örnek 1 - Örnek 2 - Örnek 3 - Örnek 4 - Örnek 5
ÖRNEK-1
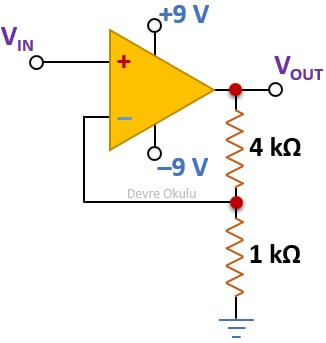
Yukarıdaki devrede OPAMP'ın ideal olduğunu ve çıkış voltajının besleme voltajları ile sınırlı olduğunu varsayarak
a) Voltaj kazancını,
b) VIN = 1 V için çıkış voltajını,
c) VIN = 3 V için çıkış voltajını,
d) VIN = –1 V için çıkış voltajını ve
e) VIN = –3 V için çıkış voltajını
bulalım.
ÇÖZÜM

a) Pozitif giriş direk olarak VIN'e bağlıdır. Bu nedenle Vp = VIN'dir. İdeal OPAMP varsayımına göre
Vn = Vp = VIN
olur. Vn voltajı aynı zamanda 1 kΩ'luk direncin üzerindeki voltaja eşittir. Buna göre, 1 kΩ'luk dirençten geçen akım aşağıdaki gibidir.
...
Negatif girişten akım geçmediği için 4 kΩ'luk direncin üzerindeki akım, 1 kΩ'luk direncin akımına eşittir.
4 kΩ'luk direncin üzerindeki voltaj
...'dir.
Çıkış voltajı da 1 ve 4 kΩ'luk dirençler üzerindeki voltajların toplamına eşittir.
VOUT = VIN + 4VIN = 5VIN
Çıkış voltajı, giriş voltajının 5 katı olduğu için bu devrenin voltaj kazancı 5'tir.
Cevap:
...
b) Çıkış voltajını bulabilmek için giriş voltajı ile voltaj kazancını çarparız.
VOUT = 5 . (1 V) = 5 V
Cevap:
VIN = 1 V için VOUT = 5 V
c) Eğer besleme voltajlarını gözardı edersek,
VOUT = 5 . (3 V) = 15 V
çıkar. Fakat bu değer pozitif besleme voltajından yüksektir. Bu nedenle, çıkış voltajı 9 V'a eşit olur.
Cevap:
VIN = 3 V için VOUT = 9 V
d) Bu soru için de, diğerlerinde olduğu gibi kazanç ile giriş voltajını çarpacağız.
VOUT = 5 . (–1 V) = –5 V
Cevap:
VIN = –1 V için VOUT = –5 V
e) Aynı yöntemle
VOUT = 5 . (–3 V) = –15 V
sonucunu buluruz. Fakat –15 V, negatif besleme voltajından küçük olduğundan, çıkış voltajı –9 V olmalıdır.
Cevap:
VIN = –3 V için VOUT = –9 V