Devrelerde, analizi kolaylaştırmak için seri bağlı dirençleri, eşdeğer direnç adını verdiğimiz tek bir dirençle değiştirebiliriz.
Seri bağlı dirençlerin eşdeğeri, bu dirençlerin toplamına eşittir.
Seri bağlı R1, R2, ..., Rn dirençlerinin eşdeğeri
Reş = R1 + R2 + ... + Rn'dir.

ÖRNEK:
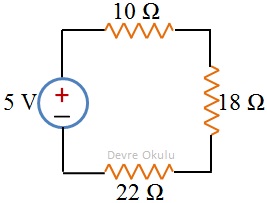
Yukarıdaki devrede seri bağlı dirençlerin eşdeğerini bulalım.
Bu devrede 10 Ω, 18 Ω ve 22 Ω'luk dirençlerin seri bağlı olduğunu görüyoruz. Bu bağlantının eşdeğeri
Reş = 10 Ω + 18 Ω + 22 Ω = 50 Ω
değerinde bir dirençtir.
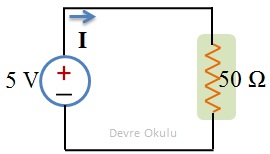
Bu üç direncin yerine voltaj kaynağına 50 Ω'luk bir direnç bağladığımızda voltaj kaynağından çıkan akım veya harcanan toplam güç değişmez.

ÖRNEK:
Tasarladığımız bir OPAMP devresinde 6.6 kΩ'luk bir dirence ihtiyaç duyduğumuzu, yalnız elimizde sadece 220 Ω, 2.2 kΩ, 2.7 kΩ ve 3.3 kΩ'luk dirençler olduğunu düşünelim. Hangi dirençleri ne şekilde bağlayarak 6.6 kΩ'luk direnç değerini elde edebiliriz?
- 2 adet 3.3 kΩ'luk direnci seri bağlayarak; veya
- 3 adet 2.2 kΩ'luk direnci seri bağlayarak; veya
- 10 adet 220 Ω'luk direnci seri bağlayarak;
istenilen değeri elde edebiliriz.
SERİ BAĞLANTIDA EŞDEĞER DİRENÇ FORMÜLÜ NEREDEN GELİYOR?

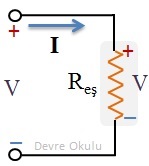
Toplam potansiyel farkı V olan ve üzerilerinden I akımı geçen n tane direncin seri bağlı olduklarını düşünelim. Devrede bu dirençlerin tümüne eşdeğer bir direnç koyduğumuzda bu direncin voltajı V ve üzerinden geçen akım I olmalıdır. Aksi taktirde, bu dirençlere eşdeğer olduğunu söyleyemeyiz.
Seri bağlı dirençlerin voltajlarını V1, V2, ..., Vn ile gösterirsek, Kirchhoff Voltaj Kanunu'nu kullanarak
V= V1 + V2 + ... + Vn
eşitliğini yazabiliriz. Eşitliğin sağındaki her bir direnç için Ohm Kanunu'nu kullanarak, voltajı akım ve direnç cinsinden yazabiliriz. (Örneğin, V1 = IR1, V2 = IR2, vb.)
V = IR1 + IR2 + ... + IRn
= I(R1 + R2 + ... + Rn)
Eşdeğer direnç üzerinden de aynı I akımı geçtiği için eşitliğin solundaki V yerine IReş yazıp, iki tarafı da I'ya böldüğümüzde, seri dirençlerin eşdeğerini veren formülü elde edebiliriz.
IReş = I(R1 + R2 + ... + Rn)
⇒ Reş = R1 + R2 + ... + Rn
Bölüm 1 - Bölüm 2 - Bölüm 3 - Bölüm 4
İlgili Bağlantılar
BÖLÜM 1-SERİ BAĞLANTI NEDİR? BÖLÜM 2-SERİ BAĞLANTIDA AKIMLAR BÖLÜM 3-SERİ BAĞLANTIDA POTANSİYEL DAĞILIMI BÖLÜM 4-SERİ BAĞLANTIDA EŞDEĞER DİRENÇ ÇÖZÜMLÜ ÖRNEKLER