TERS POLARMA (İDEAL MODEL)
(REVERSE BIAS)
Bu örneği, ideal model kullanarak çözeceğiz. Aynı sorunun pratik model ile çözümüne Diyot Devreleri-2-Ters Polarma-Pratik Model bağlantısından ulaşabilirsiniz.
Devre Şeması
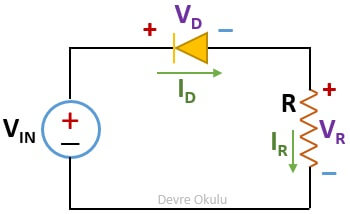

Yukarıdaki devrede, diyot için ideal model kullanarak
a) direnç üzerinden geçen akımı (IR),
b) diyot üzerinden geçen akımı (ID),
c) direnç üzerindeki voltajı (VR),
d) diyot üzerindeki voltajı (VD),
e) diyotun harcadığı gücü (PD) ve
f) direncin harcadığı gücü (PR)
bulalım.
Çözüm ve Açıklamalar
Diyotlu devrelerin analizi için, ilk olarak diyotların polarma şeklini (ters polarma, doğru veya düz polarma) bulmamız gerekiyor.
Diğer devrelerde olduğu gibi, ilk adımda diyotun doğru polarma mı, yoksa ters polarma mı olduğunu anlamaya çalışmalıyız.
Bu devrede, voltaj kaynağının pozitif terminali diyotun katotuna bağlı. Yani diyot üzerinde katot-anot yönünde bir akım yaratmaya çalışıyor. Yalnız, ideal modele göre, diyot bu yöndeki akımlara izin vermez ve ters polarma olur.
Ters polarmalı bir diyot, açık devre gibi hareket eder. Bu nedenle, aşağıdaki devrede diyot yerine açık devre koyuyoruz.
,
a) Direnç üzerindeki akım, IR
Devre tamamlanmadığından, direnç üzerindeki akım sıfır olur.
IR = 0
b) Diyot üzerindeki akım, ID
Aynı sebepten dolayı diyot üzerinden geçen akım da sıfırdır.
ID = 0
c) Direnç üzerindeki voltaj, VR
Ohm Kanunu'na göre, direnç üzerindeki voltajı, akım ve direnç değerlerinin çarpımından bulabiliriz. Yalnız, burada akım sıfır olduğundan, direnç üzerindeki voltaj düşümü de sıfır olur.
VR = 0
d) Diyot üzerindeki voltaj, VD
Devrede diyot ve direnç üzerindeki voltajların toplamı, Kirchhoff Voltaj Kanunu’na göre, besleme gerilimi olan VIN'e eşit olmalıdır. Direnç üzerindeki voltaj sıfır olduğundan, diyotun voltajı VIN'e eşit olur.
VD = VIN
e)Diyotun harcadığı güç, PD
Bir diyotun harcadığı gücü, üzerine düşen voltajla üzerinden geçen akımın çarpımından bulabiliriz.
PD = VD . ID
Diyot üzerinden akım geçmediği için, güç tüketimi de sıfırdır.
PD = VD . ID = VIN . 0 = 0
Gerçekte diyotun ne kadar güç harcadığını bulabilmek için ideal modelden daha gerçekçi bir model kullanmamız gerekir.
PD = 0
İdeal modele göre, bir diyotun harcadığı güç her iki polarma için de sıfırdır.
f) Direncin harcadığı güç, PR
Bir direncin harcadığı gücü bulmak için, üzerindeki voltajı ve üzerinden geçen akımı çarparız. Yalnız, bu devre için akım sıfır olduğundan, direncin güç tüketimi de sıfır olur.
PR = 0
Sayısal Örnekler
Sayısal Örnek 1
Diyot için ideal model kullanarak, aşağıdaki devredeki tüm akım, voltaj ve güç değerlerini bulalım.

Yukarıda bulduğumuz formülleri kullanarak, cevapları kolayca bulabiliriz.
VD = 5 V,
VR = 0,
ID = IR = 0,
PD = PR = 0
Aşağıdaki devrelerin tümünde aynı akım, voltaj ve güç değerlerini elde ederiz.