DOĞRU POLARMA (PRATİK MODEL)
(FORWARD BIAS)
Bu örneği, pratik model kullanarak çözeceğiz. Aynı sorunun ideal model ile çözümüne Diyot Devreleri-1-Doğru Polarma-İdeal Model bağlantısından ulaşabilirsiniz.
Devre Şeması
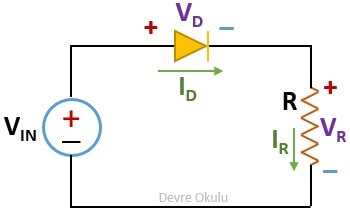

Yukarıdaki devrede, VF eşik gerilimine sahip diyot için pratik model kullanarak
a) diyot üzerindeki voltajı (VD),
b) direnç üzerindeki voltajı (VR),
c) direnç üzerinden geçen akımı (IR),
d) diyot üzerinden geçen akımı (ID),
e) diyotun harcadığı gücü (PD) ve
f) direncin harcadığı gücü (PR)
bulalım.
Çözüm ve Açıklamalar
Diyotlu devrelerin analizi için, ilk olarak diyotların polarma şeklini (ters polarma, doğru veya düz polarma) bulmalıyız.
Diyotlu bir devrede ilk yapmamız gereken şey, diyotların doğru polarma mı yoksa ters polarma mı olduğunu anlamaktır.
Pratik modelde, bir diyotun doğru polarma olabilmesi için, anota uygulanan voltaj, katota uygulanandan en az eşik gerilimi kadar fazla olmalıdır. Bu devrede voltaj kaynağının pozitif terminali anota bağlı olduğundan, anot voltajı katottan daha yüksektir. Fakat, soruda giriş voltajının eşik geriliminden yüksek veya düşük olduğuna dair bir bilgi verilmiyor. Bu nedenle, her iki durumu da ayrı ayrı ele alacağız. Eğer, VIN değeri VF’den küçükse, kaynak diyotun eşik gerilimini aşamaz ve diyot ters polarma olur. VIN > VF durumunda ise, diyot doğru polarma olur.
Bu devrede,
VIN < VF için diyot ters polarma,
VIN > VF için diyot doğru polarma olur.
Doğru ve ters polarma durumlarında, diyot yerine farklı eşdeğer devre elemanları koyuyoruz. Bu nedenle, bu durumların her biri için ayrı bir çözümümüz olacak. Önce ters polarma durumu ile başlayalım.
i) Durum 1: VIN < VF (Ters Polarma)
VIN < VF durumunda, voltaj kaynağının değeri, diyotta akım oluşturmaya yetmeyecektir. Bu nedenle diyot ters polarmadır.
Pratik model için, ters polarma durumunda diyotun eşdeğeri açık devredir.

Diyotu açık devre ile değiştirdiğimizde, yukarıdaki devreyi elde ediyoruz. Bir devreden akım geçebilmesi için, akımın kesintisiz bir yolu takip edebilmesi gerekiyor. Ancak bu devrede kesintisiz bir yol bulunmuyor. Bu nedenle, diyotun da direncin de üzerinden akım geçmez. Ya da başka bir değişle, geçen akım sıfır olur (...). Ohm Kanunu kullanarak ...'nin de sıfıra eşit olduğunu görebiliriz. ( ... formülünde ... ise, voltaj değeri de sıfır olur.)
Akım kendine bir yol bulamasa da, Kirchhoff Voltaj Kuralı, bu devre için de geçerlidir. Bu kurala göre, giriş voltajının değeri, direnç ve diyot üzerindeki voltajların toplamına eşit olur.Yani,
... ...
... olduğundan, ... voltajının tümü diyot üzerinde kalır.
Akımları sıfır olduğundan, diyotun da direnci de güç tüketimleri 0 olur. Çünkü, her ikisi için de harcanan güç, üzerlerinden geçen akımla voltajlarının çarpımıdır.
... < ... için
...,
...,
...,
...,
ii) Durum 2: VIN>VF (Doğru Polarma)
Bu devrede voltaj kaynağı, eşik değerini aşacak kadar voltaj üretirse, diyot üzerinden akım geçer ve doğru polarma olur.
Doğru polarmalı bir diyot, pratik modele göre, pozitif ucu anoda bakacak şekilde VF değerinde ideal bir voltaj kaynağı gibi hareket eder.
Diyot yerine eşdeğerini koyarak elde ettiğimiz aşağıdaki devrede, iki voltaj kaynağı ve bir direnç görebiliriz.
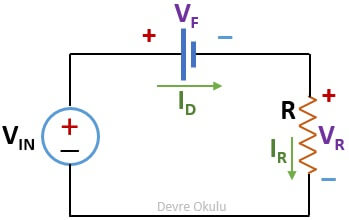
Eşdeğer devremizi elde ettiğimize göre, artık soruda istenilenleri bulabiliriz.
a) Diyot üzerindeki voltaj, VD
Pratik modelde diyot ideal bir voltaj kaynağına eşit olduğundan, üzerine düşen voltaj eşik değeri olan VF’ye eşit olur.
...
b) Direnç üzerindeki voltaj, VR
Voltaj kaynağımız ..., Kirchhoff Voltaj Kuralı’na göre diyot ve direnç üzerindeki toplam voltaja eşit olmalıdır. Diyot üzerindeki voltaj ... olduğundan, direnç üzerindeki voltaj ... değerine eşit olur.
...
c) Direnç üzerindeki akım, IR
Ohm Kanunu’nu kullanarak direnç üzerindeki akımı, ... olarak buluruz.
...
d) Diyot üzerindeki akım, ID
Aynı tel üzerinde oldukları için, diyot ve direnç üzerinden aynı miktarlarda akım geçer (...).
...
e)Diyotun harcadığı güç, PD
Bir diyotun harcadığı gücü, üzerine düşen voltaj ile üzerinden geçen akımı çarparak bulabiliriz.
...
Diyotun harcadığı güç (direnç ile aynı şekilde) üzerine düşen voltaj ve üzerinden geçen akımların çarpımıyla bulunur. Yukarıda bulunan sonuçları kullanarak,
... ...
formülünü elde ederiz.
...
İdeal model kullanıldığı durumun aksine, burada sıfırdan farklı bir değer elde ediyoruz.
f) Direncin harcadığı güç, PR
Bir direncin harcadığı gücü bulmak için, üzerindeki voltajı ve üzerinden geçen akımı çarparız.
...
Sayısal Örnekler
Sayısal Örnek 1
Aşağıdaki devrede, diyotun eşik değerinin 0.7 V olduğunu düşünelim. Pratik model kullanarak tüm akım, voltaj ve güç değerlerini bulalım.

Devreyi besleyen voltaj kaynağı, eşik değerinden büyük olduğu diyot doğru polarma olur. Devredeki değerleri Durum 2 için bulduğumuz formüllerde yerine koyarak soruyu kolayca çözebiliriz.
...,
...,
...,
...,
...,
Birim çevrimlerine dikkat edelim. (V/Ω = A), (V/kΩ = mA), (V . A = W), (V . mA = mW)
Sayısal Örnek 2
Aşağıdaki devrede, diyot için pratik model kullandığımızı ve eşik değerinin 0.7 V olduğunu varsayalım. Kullanılan direncin maksimum güç tüketimi, 0.25W olsun. Bu durumda direncin yanmaması için maksimum kaç voltluk bir kaynak kullanılabilir? (Bu örnek için diyotun maksimum güç tüketimini göz ardı edelim.)

Devredeki diyot, voltaj kaynağı diyotun eşik değerinden fazla olduğundan, doğru polarmadır. Diyot yerine 0.7 V değerinde bir voltaj kaynağı koyabiliriz. (Voltaj kaynağının yönünü doğru koymak oldukça önemli. Pozitif terminal anot tarafında olmalı.)
Böylece direncin akımını, ... ve voltajını ise ... olarak buluruz.
Direncin güç tüketimini ise akım ve voltaj değerlerinin çarpımı ile bulabiliriz.
...
Maksimum giriş voltajını bulabilmek için güç yerine 0.25 W koyarsak,
...
eşitliğine ulaşırız.
Dolayısıyla,
... ve
... olarak bulunur.
Sonuç olarak, direncin yanmaması için maksimum gerilim voltajı ... olur.
16.51 V
Sayısal Örnek 3
Sayısal Örnek 2’deki devrede, diyotun ve direncin maksimum güç tüketimleri sırasıyla 0.5 W ve 0.25 W ise, devre elemanlarının herhangi birinin yanmaması için devreye en fazla kaç voltluk bir besleme gerilimi uygulanabilir?
Bir önceki soruda, sadece direncin güç tüketimi göz önünde bulundurulduğunda, maksimum besleme gerilimi ... olarak bulunmuştu. Şimdi ise, direncinkini göz ardı edip, diyotun maksimum güç tüketimine ulaşmak için gerekli olan besleme voltajını bulalım.
Bu devre için diyot üzerinde harcanan güç
...
olur.
...’ı bulabilmek için, ...'yi diyotun maksimum güç tüketimi olan 0.5 W değerine eşitleyeceğiz.
...
Bu eşitlikteki düzenlemelerle, ... sonucunu buluruz.
Bu noktada, ... için iki değer bulmuş olduk. Birisi 16.51 V, diğeri ise 714.99 V. Eğer besleme voltajı 16.51 V’dan büyükse, direnç yanar ama 714.99 V’a kadar diyot sağlam kalır. Eğer bu değer 714.99 V’dan büyükse her iki devre elemanı da yanar. Bu soruda istenilen hem diyotun hem de direnci sağlam kalması olduğundan cevabımız bu iki değerin küçük olanı, yani 16.51V olmalıdır.
16.51V