DOĞRU POLARMA (İDEAL MODEL)
(FORWARD BIAS)
Bu sayfadaki örnekleri ideal model kullanarak çözüyoruz. Aynı soruların pratik model ile çözümlerine Diyot Devreleri-1-Doğru Polarma-Pratik Model bağlantısından ulaşabilirsiniz.
Devre Şeması
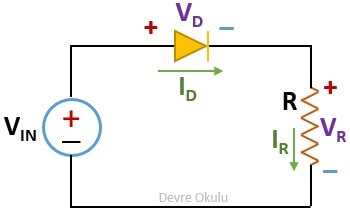

Yukarıdaki devrede, diyot için ideal model kullanarak
a) diyot üzerindeki voltajı (VD),
b) direnç üzerindeki voltajı (VR),
c) direnç üzerinden geçen akımı (IR),
d) diyot üzerinden geçen akımı (ID),
e) diyotun harcadığı gücü (PD) ve
f) direncin harcadığı gücü (PR)
bulalım.
Çözüm ve Açıklamalar
Diyotlu devrelerin analizinde, ilk olarak, diyotların polarma şeklini (ters polarma, doğru veya düz polarma) bulmamız gerekir.
Diyotlu bir devrede, ilk olarak, diyotların doğru polarma mı yoksa ters polarma mı olduğunu bulmamız gerekiyor. Bu adımı tamamladıktan sonra, kullandığımız modele göre, diyotların yerlerine eşdeğer devre elemanlarını yerleştiriyoruz. Son olarak, elde ettiğimiz devrede temel devre analizinde kullanılan kural ve kanunları kullanıyoruz.
İlk adım olan polarma türünü bulmakla, çözüme başlıyoruz. Çok fazla diyot ve devre elemanı olan bir devre için, diyotların polarma yönünü bulmak, oldukça karmaşık bir problem haline dönüşebilir. Bu durumlarda, polarma şekline dair varsayımlarda bulunup, analize devam edebiliriz. Yalnız, bu analizin sonucu, başlangıçta yaptığımız varsayımların yanlış olduğunu da gösterebilir. Bu durumda, tekrar başa dönüp, analiz sonuçları ile varsayımlarımızın çelişmediği bir durum bulana kadar, yeni varsayımlarla ilerlememiz gerekiyor.
Ama, neyseki bu basit devrede, diyotun doğru polarma olduğunu görebilmek için detaylı bir analiz yapmamıza gerek yok. Devrede yalnızca bir diyot var ve devre polarma yönü için bize açık ipuçları sunuyor. Yalnızca bir (voltaj) kaynağımız olduğu için, devrede dolanan tüm akım, bu kaynağın pozitif terminalinden başlamalı. Akımın negatif terminale ulaşana kadar katedeceği yol için de, karşımıza yalnız bir seçenek çıkıyor, o da akımın önce diyot, daha sonra da direnç üzerinden geçmesi. Diyot üzerinden geçen akımın yönü bu durumda anot-katot doğrultusunda, yani diyotun izin verdiği yönde oluyor. Bu nedenle, diyotun bu devrede doğru polarmada olduğunu söyleyebiliriz.
Doğru polarmalı bir diyot, ideal modele göre, kısa devre (direnci sıfır olan bir tel) gibi hareket eder. Bu nedenle, diyot yerine kısa devre koyarak, analize devam edebiliriz.
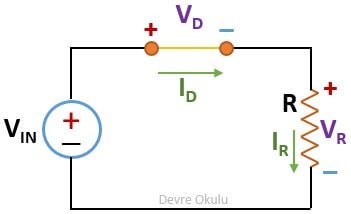
Diyotun yerine, eşdeğeri yerleştirilmiş yukarıdaki devrede, sadece bir voltaj kaynağı ve bu voltaj kaynağına bağlı bir direnç görüyoruz. Artık Ohm Kanunu kullanarak istenilen değerlere kolayca ulaşabiliriz.
a) Diyot üzerindeki voltaj, VD
İdeal modelde diyotun eşdeğeri kısa devre olduğundan, üzerindeki voltaj 0’dır (VD = 0). Bunu Ohm Kanunu'nu kullanarak da görebiliriz. Ohm Kanunu’na göre R değerinde bir direnç üzerinden I akımı geçiyorsa, üzerindeki voltajı
V = I × R
formülü ile elde edebiliriz. Kısa devre için R = 0’dır. Bu nedenle, akımın değeri ne olursa olsun, kısa devre üzerine düşen voltaj sıfırdır.
VD = 0
b) Direnç üzerindeki voltaj, VR
Voltaj kaynağımızın ürettiği gerilim olan VIN, Kirchhoff Voltaj Kuralı’na göre diyot ve direnç üzerindeki toplam voltaja eşit olmalıdır.
VIN = VD + VR
Diyot üzerindeki voltaj sıfır olduğundan, direnç üzerindeki voltaj, VIN değerine eşit olur.
VR = VIN
c) Direnç üzerindeki akım, IR
Ohm Kanunu’nu kullanarak direnç üzerindeki akımı, ... olarak buluruz. ... olduğundan, ... çıkar.
...
d) Diyot üzerindeki akım, ID
Aynı tel üzerinde oldukları için, diyot ve direnç üzerinden aynı miktarlarda akım geçer (...). Dolayısıyla, bir önceki cevabın aynısını elde ederiz.
...
e)Diyotun harcadığı güç, PD
Bir diyotun harcadığı gücü, üzerine düşen voltaj ile üzerinden geçen akımı çarparak bulabiliriz.
...
Diyotun harcadığı güç (direnç ile aynı şekilde) üzerine düşen voltaj ve üzerinden geçen akımların çarpımıyla bulunur. Yukarıda bulunan sonuçları kullanarak,
... ...
formülünü elde ederiz. Yalnız, bu formülde ... değeri 0’a eşit olduğundan, ... olur. Bu sonuç, bize ideal modele göre diyot üzerinde güç harcanmadığını söylemektedir. Ancak, idealleştirilmiş bir devrede böyle bir sonuç elde etmemiz, gerçekte diyotun güç harcamadığı anlamına gelmez. Gerçekte diyotun ne kadar güç harcadığını bulabilmek için ideal modelden daha gerçekçi bir model kullanmamız gerekir.
0
İdeal modele göre, bir diyotun harcadığı güç her iki polarma için de sıfırdır.
f) Direncin harcadığı güç, PR
Bir direncin harcadığı gücü bulmak için, üzerindeki voltajı ve üzerinden geçen akımı çarparız.
...
Sayısal Örnekler
Sayısal Örnek 1
Aşağıdaki devrede diyotun ideal olduğunu varsayarak, tüm akım, voltaj ve güç değerlerini bulalım.

Bu soruda verilen değerleri, yukarıda bulduğumuz formüllerde yerine koyarak, cevaplara kolayca ulaşabiliriz.
VR = 5 V,
VD = 0 V,
ID = IR = 5 mA,
PD = 0 W,
PR = 25 mW
Birim çevrimlerine dikkat edelim. (V/Ω = A), (V/kΩ = mA), (V . A = W), (V . mA = mW)
Sayısal Örnek 2
Aşağıdaki devre için, akım ve voltaj değerlerini bulalım.
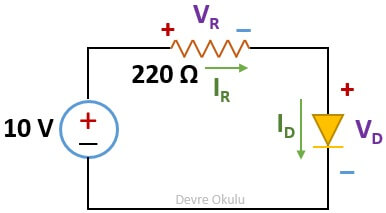
Sayfanın başındaki devre ile bu devrenin tek farkı, direnç ve diyotun yer değiştirmiş olmasıdır. Bu devreyi analiz ettiğimizde, sonuçların aynı formüllerle bulunabileceğini göreceğiz.
Aşağıdaki devrelerde voltaj, akım ve güç değerleri aynıdır.



İlk olarak, işe polarma şeklini bulmakla başlayalım.
Daha önceki devrelerimizde olduğu gibi, burada da voltaj kaynağının pozitif terminalinden başlayıp, negatif terminaline ulaşan tek bir yol var. Ve bu yolun doğrultusu diyotun anot-katot yönünde. Bu nedenle devredeki diyot doğru polarmadır.
İdeal modelde, doğru polarma bir diyot kısa devreye eşit olduğundan, devreye diyot yerine kısa devre yerleştirelim. Böylece, yine bir voltaj kaynağı ve bir dirençten oluşan aşağıdaki devreyi elde etmiş oluyoruz.

Yukarıdaki devrede, Ohm Kanunu’nu kullanarak, eşit olan ... ve ... akım değerlerini ... olarak buluruz. Doğru polarma olduğundan, diyot üzerine düşen voltaj ... ve direnç üzerine düşen voltaj ... olur.
...,
...,
...
Sayısal Örnek 3
Aşağıdaki devrede diyot için ideal model kullandığımızı varsayalım ve kullanılan direncin maksimum güç tüketimi 0.25W olsun. Bu durumda direncin yanmaması için en fazla kaç voltluk bir kaynak kullanılabilir?

Devredeki diyot düz polarmadır. İdeal model kullanıldığımızdan, diyot yerine kısa devre koyabiliriz ve bu durumda devreden geçen akım,
... ve direncin voltajı ... olur.
Direncin güç tüketimi ... eşitliği ile bulunur. ... için maksimum değer 0.25 W olduğundan, maksimum giriş voltajını bulabilmek için güç yerine 0.25 W koyarsak,
... olur.
Bu formülden ...’ı çekersek,
...
sonucuna ulaşırız.
Böylece direncin maksimum güç tüketimini geçmemesi için, voltaj kaynağından uygulayabileceğimiz en yüksek voltajı 15.81 V olarak buluyoruz. Daha yüksek giriş voltajları için direnç yanacaktır.
15.81V
İlgili Bağlantılar
ÇÖZÜMLÜ ÖRNEKLER ÖRNEK 1A(İDEAL MODEL) ÖRNEK 1B(PRATİK MODEL) ÖRNEK 2A(İDEAL MODEL) ÖRNEK 2B(PRATİK MODEL) ÖRNEK 3A(İDEAL MODEL) ÖRNEK 3B(PRATİK MODEL) ÖRNEK 4A(İDEAL MODEL) ÖRNEK 4B(PRATİK MODEL) ÖRNEK 5A(İDEAL MODEL) ÖRNEK 5B(PRATİK MODEL)