KONU 5-PARALEL DİRENÇLER
BÖLÜM 3-PARALEL BAĞLI DİRENÇLERİN EŞDEĞERİ
Seri bağlantıya benzer şekilde, paralel bağlı dirençlerin yerine de bu dirençlere eşdeğer bir direnç bulabiliriz.


Paralel bağlı R1, R2, …, Rn dirençlerinin eşdeğeri
... ... ... ...
formülü ile bulunur.
ÖRNEK:

Yukarıdaki devrede paralel bağlı dirençlerin eşdeğerini bulalım.
Bu devrede 2 kΩ, 3 kΩ ve 6 kΩ’luk dirençler paraleldir. Bu dirençlerin eşdeğerini
... ... ... ...
formülü ile bulabiliriz. Paydaların tümü 6 kΩ olacak şekilde bir genişletme yaparsak,
... ... ... ... ... ...
olduğunu buluruz. Eşitliğin her iki tarafında pay ile paydanın yerini değiştirerek
Reş = 1 kΩ
sonucunu elde ederiz.
Paralel Bağlantıda Eşdeğer Direnç Formülü Nereden Geliyor?
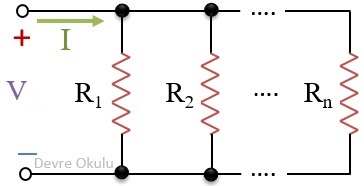

Paralel bağlı n tane direncin, ortak terminalleri arasında V potansiyel farkı olduğunu ve bu devrenin ana kolundan I akımının geçtiğini düşünelim.
Bu dirençlerin yerine koyacağımız direncin paralel dirençlere eşdeğer olabilmesi için voltajının V ve üzerinden geçen akımın I olması gerekir.
Paralel oldukları için bu devredeki tüm dirençlerin voltajları V’ye eşittir. Ohm Kanunu’nu kullanarak, her bir direnç üzerindeki akımı
..., ...,…, ...
olarak bulabiliriz.

Yukarıdaki devrede, A düğümüne giren tek akım ana koldaki ... akımıdır. Çıkan akımların toplamı ise ...’dir. Kirchhoff akım kuralına göre bir düğüme giren toplam akım, bu düğümden çıkan akımların toplamına eşit olmalıdır.
... ...
Bu eşitlikte, ..., ..., …., ... yerine Ohm Kanunu’nu kullanarak bulduğumuz ifadeleri koyarsak, denklem
... + ... + … + ...
haline dönüşür.
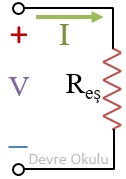
... akımının aynı zamanda Reş üzerinden de geçmesi gerektiği için yukarıdaki denklemde ... yerine ... yazabiliriz.
... ... ... ...
Eşitliğin iki tarafındaki V’leri sadeleştirdiğimizde eşdeğer direnç formülünü elde ederiz.
... ... ... ...
EŞDEĞER İLETKENLİK
İletkenlik, direncin çarpmaya göre tersidir ve G ile gösterilir.
...
Eşdeğer direnç formülünde, direnç yerine iletkenlikleri kullanırsak, bu formülü daha basit bir şekilde yazabiliriz.
Geş = G1 + G2 + … + Gn
Bu formülde
- Geş, eşdeğer direncin iletkenliği ve
- Gi ise, i’ninci direncin iletkenliğidir.
Eşdeğer iletkenlik, paralel dirençlerin iletkenliklerinin toplamına eşittir.
Matematiksel olarak bir fark olmasa da, eşdeğer direnci bulabilmek için iletkenlikleri toplayıp, çarpmaya göre tersini alabiliriz.
Bölüm 1 - Bölüm 2 - Bölüm 3 - Bölüm 4 - Bölüm 5