KONU 5-PARALEL DİRENÇLER
BÖLÜM 5-PARALEL BAĞLANTIDA AKIM DAĞILIMI
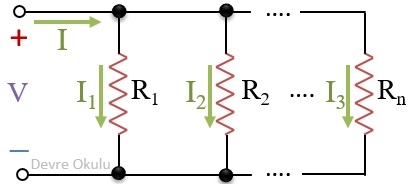
⚡ Ortak terminaller arasındaki voltaj farkının (...’nin) değerini biliyorsak, paralel bağlı R1, R2,..., Rn dirençlerinden geçen akımları
..., ..., ..., ...
formülleriyle bulabiliriz.
⚡ Ana koldan geçen ... akımının değerini biliyorsak, dirençlerin her birinden geçen akımları
..., ...,..., ...
formülleriyle bulabiliriz.
NEDEN?
Hem paralel bağlı dirençlerin hem de bu bağlantıya eşdeğer olan ... direncinin üzerinde aynı voltajı görürüz. Bir ... direncinin üzerinden geçen akımı ... ve ana koldan geçen akımı ... ile gösterirsek,
- ... direncinin akımı ... ve
- ... direncinin akımı ...
olur. Bu iki ifadeyi eşitlediğimizde
...
formülünü elde ederiz.
İKİ DİRENÇLİ PARALEL BAĞLANTI
Sadece iki direncin paralel olduğu durumda, yukarıda elde ettiğimiz formülleri basitleştirebiliriz. Paralel ... ve ... dirençlerinden geçen akımlar, sırasıyla, ... ve ... olsun. Bu akımların toplamı ... ise,
... ve ...
olur. Bu denklemleri yukarıdaki formülde ...’in yerine ... yazarak elde edebiliriz.
ÖRNEK:
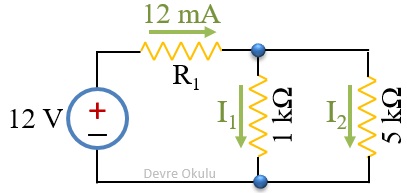
Yukarıdaki devrede ... üzerinden geçen akım 12 mA ise, 1 kΩ ve 5 kΩ’luk dirençler üzerinden ne kadar akım geçer?
Bu devrede, 1 kΩ ve 5 kΩ’luk dirençler üzerinden geçen toplam akım 12 mA’dir. ... = 12 mA, ... = 1 kΩ ve ... = 5 Ω değerlerini yukarıdaki formüllerde yerlerine yazarsak,
... ... ... ...
... ... ... ...
sonuçlarını elde edebiliriz. Bu işlemlerde 1 kΩ’luk direnç üzerinden geçen akımı ... ve 5 kΩ’luk direnç üzerinden geçen akımı ... ile gösteriyoruz.
Yukarıdaki örnekte gördüğümüz gibi, değeri düşük olan direnç akımın daha büyük bir kısmını alır.
ÖRNEK:

Yukarıdaki devrede R1 üzerinden geçen akım 8 mA’se , ... kaç miliamperdir?
Paralel bağlı eşit dirençlerin eşdeğerini bulabilmek için bir direncin değerini direnç sayısına bölebiliriz.
...
... ve ... için ... formülünü kullanarak
...
sonucunu elde ederiz.
Bölüm 1 - Bölüm 2 - Bölüm 3 - Bölüm 4 - Bölüm 5
İlgili Bağlantılar
BÖLÜM 1-PARALEL BAĞLANTI NEDİR? BÖLÜM 2-PARALEL BAĞLANTIDA VOLTAJLAR BÖLÜM 3-PARALEL BAĞLI DİRENÇLERİN EŞDEĞERİ BÖLÜM 4-EŞDEĞER DİRENCİN ÖZELLİKLERİ BÖLÜM 5-PARALEL BAĞLANTIDA AKIM DAĞILIMI ÇÖZÜMLÜ ÖRNEKLER